Vous vous êtes surement déjà posé la question de savoir comment adapter le temps de cuisson à la taille d’une pièce à rôtir (chapon, gigot), ou adapter les quantités d’une recette à la taille du moule.
Cet article devrait vous aider. Et ne vous laissez pas impressionner par les formules. On n’est pas obligé de tout comprendre !
La version courte
La diffusion de la chaleur dans un aliment ne dépend pas de son poids, mais de son épaisseur ! C’est essentiel à savoir
- pour adapter les temps de cuisson (pour cuire un chapon par rapport à un poulet),
- pour adapter les quantités d’une recette (pour cuire un fondant dans un moule de 16 cm au lieu de 24 cm),
- ou pour estimer le temps de cuisson à basse température (pour le fameux gigot de 11 heures !)
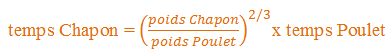
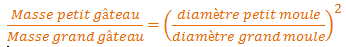
Pas de panique ! La plupart des téléphones portables ont des calculatrices qui vous permettront de faire facilement les calculs.
Que nous dit la science ?
La loi de diffusion thermique
Quel que soit l’objet que l’on chauffe (acier, rôti de bœuf, tarte, huile, eau, etc.), il existe une loi de diffusion thermique qui dit que « le temps nécessaire à la chaleur pour diffuser dans un aliment est égal au carré de la distance parcourue divisé par le coefficient de diffusion thermique de ce corps (on parle parfois de coefficient de diffusivité thermique).
Sous forme d’équation, ça s’écrit t = L2/D où
- t est le temps de diffusion de la chaleur (en secondes),
- L est la distance parcourue par la chaleur (en mètres ou centimètres, ou millimètres)
- D est le coefficient de diffusivité thermique du corps chauffé (en m2 par seconde, ou cm2 par seconde, ou mm2 par seconde).
Donc pour faire chauffer de l’eau plus rapidement, il vaut mieux utiliser une casserole large, dans laquelle la hauteur d’eau sera moins importante.
Quand on cuit un aliment au four (entrecôte, rôti, poulet, dinde, gâteau, etc.), la chaleur se propage par le dessus et le dessous.
Dans ce cas, la distance que doit parcourir la chaleur est la moitié de son épaisseur. La loi de diffusion thermique devient donc t = L2/4D où L est l’épaisseur totale de l’aliment.
Cette règle est valable aussi quand on cuit à la poêle ou au barbecue, à condition de retourner l’aliment régulièrement pour qu’il soit chauffé des 2 côtés.
Vous remarquerez que cette loi ne parle pas du poids de l’aliment. C’est donc bien l’épaisseur qui est importante !
Mais vous le saviez déjà ! Quand vous cuisez 3 steaks hachés dans une poêle, vous ne les cuisez pas 3 fois plus longtemps qu’un seul steak, n’est ce pas ? (à condition bien sûr de ne pas les empiler les uns sur les autres …)
Alors la prochaine fois que votre boucher vous dira que le temps de cuisson de votre rôti c’est « un quart d’heure par livre », parlez-lui de la loi de diffusion thermique !
Et expliquez-lui (gentiment) que s’ils ont la même épaisseur, un rôti de 700g et un rôti de 2kg demandent le même temps de cuisson.
Quelles implications en cuisine ?
Adapter le temps de cuisson
Imaginons que vous ayez une recette favorite pour cuire votre poulet dominical de 1.5kg, et que vous ayez l’habitude de le cuire dans un four à 200°C pendant 1h30.
Pour Noël, vous décidez de préparer une dinde ou un chapon qui pèsent 3kg. Quelle devra être le temps de cuisson à 200°C ?
On imagine que le poulet, le chapon ou la dinde sont des sphères (des boules). La distance que devra parcourir la chaleur jusqu’au centre de la volaille est donc le rayon de la sphère.
Et comme un poulet, une dinde ou un chapon ont tous la même masse volumique (en g/m3), alors la distance que devra parcourir la chaleur est proportionnelle au poids de la sphère à cuire. Et finalement, le rapport des temps de cuisson sera également proportionnel au rapport des poids.
Pour le calcul, la formule est donc :
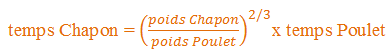
Et il vous suffira de remplacer « Chapon » par « Dinde », ou « Caille », ou « Dinosaure » dans la formule pour calculer le temps de cuisson correspondant.
En chiffres, le temps de cuisson de la dinde ou du chapon sera de 1.6 fois le temps de cuisson du poulet, soit 2h20mn.
Si vous aviez utilisé le rapport des poids (la dinde ou le chapon pèsent 2 fois plus lourd que votre poulet), vous auriez cuit pendant 3h et votre dinde ou votre chapon aurait été trop cuit !
Et c’est la même chose pour des œufs à la coque ! Si vous avez l’habitude de cuire vos œufs de poule (qui pèsent environ 50g) pendant 3mn pour qu’ils soient « à la coque », alors il faudrait cuire des œufs de cane (qui pèsent environ 70g) pendant 3mn 45s, des œufs d’oie (qui pèsent environ 150g) pendant 6mn 14s, et des œufs d’autruche (qui pèsent 1kg) pendant 22mn !
Si vous aviez considéré le poids de l’œuf d’autruche (qui pèse 20 fois plus que l’œuf de poule) vous l’auriez cuit pendant 1 heure !
Adapter les quantités à la taille du récipient
Imaginons qu’on vous donne une recette pour un délicieux fondant au chocolat.
La personne qui vous l’a donnée utilise un moule à manqué de 24 cm de diamètre, et cuit son fondant dans un four à 180°C pendant 40 minutes.
Malheureusement, vous n’avez qu’un moule de 16 cm de diamètre. Alors, comment adapter les proportions à la taille de votre moule ?
Pour un fondant, le plus important est le temps de cuisson. La loi de diffusion thermique nous dit que si on veut garder le même temps de cuisson, alors il faut garder la même hauteur de l’appareil dans le moule (la chaleur devra parcourir la même distance).
Comme les deux préparations (appareils) contiennent les mêmes ingrédients, ils ont la même masse volumique. Donc finalement, le rapport entre les poids des 2 appareils sera égal au carré du rapport des deux diamètres (16/24).
Pour le calcul, la formule est donc:
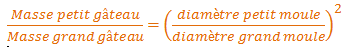
En chiffres, le poids du « petit » gâteau sera donc égal à 0.44 fois le poids du « grand » gâteau. Il faudra donc prendre 44% des quantités de la recette initiale pour chaque ingrédient (ou multiplier toutes les quantités par 0.44).
Si vous aviez fait le rapport entre les diamètres des 2 moules (16/24) vous auriez pris 66%des quantités initiales. Vous auriez eu trop d’appareil, et avec une hauteur plus grande (précisément 1.5 fois plus grande).
Et donc soit votre moule n’aurait pas pu contenir tout l’appareil, soit le fondant n’aurait pas été assez cuit.
Le gigot de 11 heures ou la cuisson à basse température
Quand on cuit une viande à basse température, on cherche à obtenir une température à cœur de 60°C, qui permet la dissolution du collagène pour attendrir la viande, sans perdre d’eau.
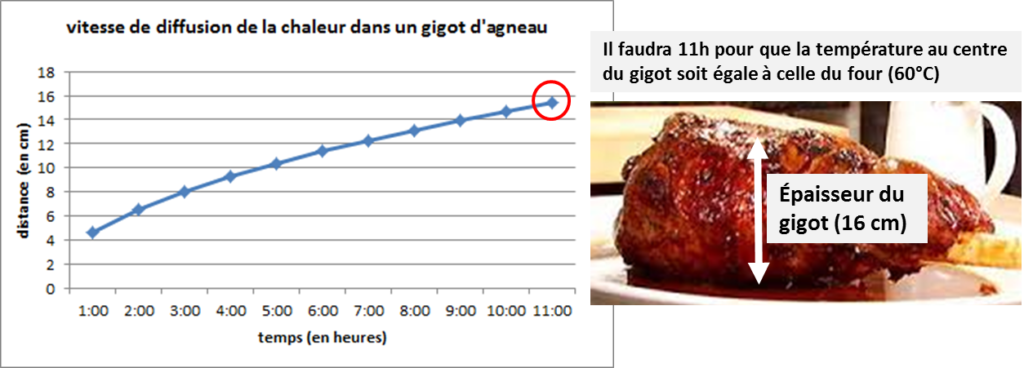
Si on met un gigot d’agneau qui fait environ 16 cm d’épaisseur dans un four à 60°C (ou dans un bac à cuisson sous-vide avec une eau à 60°C), il faudra environ 11h pour que le centre du gigot soit à 60°C.
Il suffira ensuite de le faire revenir quelques minutes dans une poêle ou sous le grill – pour lui donner un bon goût de grillé à l’extérieur- et déguster un gigot ultra fondant et goûteux !
Certaines recettes indiquent des temps de cuisson plus court (souvent 4h), parce que la température du four recommandée est supérieure (souvent 80°C) et que le gigot est d’abord saisi à la poêle pendant 15 à 20 mn, ce qui augmente la température à l’intérieur du gigot.
Mais dans ce cas, la partie extérieure du gigot sera plus cuite et plus sèche. Si vous avez le temps, préférez une cuisson plus longue à plus basse température !
Les références
Les documents suivants m’ont aidé à préparer cet article. Que leurs auteurs en soient remerciés
- Wikipedia: diffusivité thermique
- Michael Brenner, Harvard. voir la vidéo
- Vidéo de démonstration d’une application développée par le MIT (Massachusetts Institute of Technology) pour modéliser la cuisson de la viande voir la vidéo
Détails des calculs
Insert du 11 avril 2018 : il y avait une erreur dans la formule du volume de nos gâteaux. Bravo et merci à G. Michael pour sa vigilance. Heureusement, pas d’incidence sur vos calculs de proportionnalité !
Insert du 12 mars 2023 : il y avait une erreur de frappe dans le déroulé des calculs pour le calcul du temps de cuisson (volume des sphères). Heureusement, pas d’incidence sur les calculs de proportionnalité présentés dans l’article. Bravo et merci au lecteur (anonyme) qui a signalé cette erreur.
En plus d un thermomètre de cuisson il va donc falloir que j investisse dans un mètre de couturière; -).
Pas vraiment besoin. La taille des moules est habituellement gravée sur le fond. Une balance par contre c'est très utile !
pour le calcul du volume d'un cylindre c'est le rayon qui est à prendre en compte, pas le diamètre…
Très juste ! Désolé pour l'erreur. Heureusement, ça ne change pas les résultats des calculs de proportionnalité !
Bjr
Je ne comprends pas l’histoire du poulet et du chapon!!
On sait que Rpoulet au carré = 4Dxt poulet et idem pour chapon
Donc le quotient de R poulet au carré sur R chapon au carré sera égal au quotient 4Dx tpoulet sur 4D tchapon, donc tpoulet sur tchapon. D’où vient cette puissance 2/3 ?? À quel endroit ai-je arrêté de comprendre ??
Bonjour. On cherche une formule qui lie le temps de cuisson au poids. Et pour cela, il faut utiliser l'égalité des masses volumiques. Et comme les temps sont proportionnels au carré des rayons R, et que les volumes sont proportionnels au cube des rayons, on retrouve donc au final la puissance 3/2 ou 2/3 entre les temps et les poids. N'hésitez pas à reprendre la démonstration pas-à-pas à la fin de l'article. Et si vous bloquez toujours, n'hésitez pas à revenir vers moi. Bon courage !
Quelle formule pour une recette initiale pour un moule de 16cm pour un moule de 24 cm.?
Bonjour. C'est l'inverse de la formule présentée dans l'article et qui permet de passer d'un moule de 24 cm à un moule de 16 cm. Dans votre cas, il faudra augmenter les quantités de 225% (ou tout multiplier par 2.25) qui est le carré de 24/16.
Désolée je n’ai pas fait maths sup alors je fie à mon instinct
Bonjour. Ne soyez pas désolée. Je n’ai pas fait Maths sup non plus 😉. L’idée de cet article est d’aider les lecteurs à éviter les erreurs et à comprendre pourquoi certaines intuitions ne sont pas « bonnes ». Par exemple que la durée de cuisson au four dépend de l’épaisseur et non pas du poids. Et j’ai fait attention à proposer des formules simples, que l’on peut appliquer sans avoir besoin de comprendre tout leur développement.
j’ai (heureusement) un piano avec un grand four. J’ai 3 poulardes d’environ 4kilos chacun + la farce. Je sais que ce n’est pas 3 fois plus long – est-ce que quelqu’un peut m’aider ??
Bonjour,
Quelle est votre question exactement ? Si c’est de savoir le temps de cuisson des 3 poulardes en même temps par rapport à 1 seule, je dirais sensiblement le même temps si vous enfournez dans un four suffisamment préchauffé. Il faudra surveiller la cuisson à la fin du temps et peut-être prolonger légèrement.
N’hésitez pas à commenter si ne n’était pas votre question.
Bonjour, j’ai un rôti de boeuf à cuire. Je veux connaître le temps de cuisson mais comment on trouve D?
Mon rôti fait 10cm de haut ( L )
Bonjour. Merci pour votre message. Le coefficient D de diffusivité thermique de la viande de boeuf est de 1.35 x 10-3 cm2/s. Il est proche de celui de l’eau (1.5 x10-3 cm2/s) car la viande contient entre 65% et 70% d’eau.
Donc le temps de diffusion de la chaleur dans votre rôti sera de 18.518 secondes, soit environ 5h.
Mais attention ! Ce temps signifie que si vous mettez votre rôti dans un sac sous-vide et dans une eau maintenue à 55°C, il faudra 5h pour que le cœur soit à 55°C (saignant), comme le reste du rôti. C’est le principe de la cuisson à basse température.
Pour une cuisson au four, je vous recommande de le mettre dans un plat au four à 100°C pendant environ 1h, en surveillant la cuisson avec un thermomètre placé au cœur. Dès que la température atteint les 55°C, vous sortez le rôti. Il vous suffira ensuite de le sécher et de le faire revenir dans de l’huile chaude dans une poêle pour avoir un extérieur grillé et un cœur saignant.
Tenez nous au courant du résultat, et si possible chronométrez le temps de cuisson.
Bonjour, n’y a t’il pas une erreur dans la formule du volume d’une sphère ? C’est exposant 3 et pas 2.
Bonjour. Bien vu ! Il y avait bien une faute de frappe dans le déroulé du calcul en fin d’article sur les volumes des sphères. Heureusement, la formule résumée présentée dans l’article est correcte. Bravo et merci pour votre vigilance !
Bonjour je suis un peu perdue dans la formule pour le chapon je ne comprends pas pourquoi le 4D disparaît je n’ai pas bien compris l’intérêt du début de la démonstration?
Et je ne comprends pas comment le D se calcule?🧐
Bonjour. Merci pour votre message. Je vais essayer de vous apporter des éclaircissements.
1) concernant D (le coefficient de diffusivité thermique), c’est une valeur qui se mesure en laboratoire pour chaque matériau. Vous pouvez chercher sur internet si vous voulez plus d’informations. En cuisine, on admet que les plats se comportent comme de l’eau qui est leur principal constituant. Et pour l’eau, D = 1.5×10-7 m2/s.
2) concernant la démonstration, l’objectif est de calculer le temps de cuisson pour une pièce (ici un chapon) quand on connait le temps de cuisson pour une autre pièce (ici un poulet), et le poids respectif de chaque pièce. Je vous invite à suivre pas-à-pas la démonstration présentée à la fin de l’article.
En résumé on procède en 3 étapes :
Au final, on démontre que le rapport des temps de cuisson n’est pas simplement le rapport des masses.
J’espère vous avoir éclairé(e).
Cordialement,
Merci beaucoup c’est vrai que c’est plus clair maintenant! Merci de m’avoir un peu plus éclairée.
Quel est le temps de cuisson en fonction de la température du four ? en supposant qu’on enfourne à 20°, ou autre ?
Merci à vous
Bonjour,
Merci pour votre question. Je me suis posé la même quand j’ai écrit ce post. Malheureusement, je n’ai pas trouvé la réponse.
La loi de diffusion thermique nous donne le temps que met la chaleur pour se propager dans un aliment. Et donc le temps qu’il faudra pour que la chaleur du four atteigne le coeur de la pièce. Voir l’exemple du gigot de 11h.
Mais je n’ai pas trouvé de formule qui permette de savoir la température qu’il fera dans un aliment à un instant t en fonction de la température du four.
Il existe une application développée par le MIT (http://up.csail.mit.edu/science-of-cooking/) qui permet de le simuler, mais ils ne donnent pas de détails sur les formules utilisées. Je comprends que c’est de la thermodynamique de haut niveau. Cette application peut néanmoins vous aider si besoin.
Si quelqu’un a les formules, je suis preneur !
Cordialement
merci de votre réponse rapide
Bonjour, je me pose une question et je comprend pas vraiment grand chose à vos calculs 😁, pardon.. J’ai 2 rôti de porc de 500g à cuire ensemble comment je calcul le temps de cuisson svp sachant qu’ils préconise 1h /500g
Bonjour,
Merci pour votre message. Le temps de cuisson dépend de l’épaisseur du rôti, pas de son poids. Imaginez que vos 2 rôtis soient « attachés » en un rôti plus long. Donc si vos 2 rôtis ont la même épaisseur, le temps de cuisson sera le même pour 1 rôti ou 2 rôtis.
N’oubliez pas de laisser les rôtis reposer une 15aine de minutes après la cuisson avant de les trancher. Ca laisse le temps aux jus de se répartir dans la viande (ils ont été chassés vers l’intérieur par la contraction des fibres musculaires). Sinon tout le jus va se retrouver dans le plat et la viande sera plus sèche.
Bon appétit !
quand dans une recette on donne pour un plat une temperature de 200°c et une duree de 30mn, la cuisson est-elle la même dans tous les fours?
Bonjour,
Merci pour votre question. Concernant la température du four, plusieurs éléments sont à prendre en considération
* la « justesse » du four : respecte-t-il bien la consigne de température ? Certains oui, d’autres non. Si vous avez un thermomètre de cuisine avec une sonde, vous pouvez tester votre four en le réglant sur 150°C, puis sur 200°C, et en vérifiant la température réelle grâce au thermomètre.
* le type de chauffage : les fours modernes proposent presque tous une chaleur ventilée, qui transmet plus de chaleur que la chaleur statique. La recette devrait préciser le type de chaleur, mais beaucoup ne le précisent pas. Et on considère que la chaleur ventilée chauffe à 20°C de plus que la chaleur statique pour une même température indiquée. Si la recette est ancienne, il est probable que la chaleur soit statique. si vous utilisez de la chaleur ventilée, réduisez de 20°C.
* la position dans le four : comme le four chauffe essentiellement par le rayonnement de ses parois, la position de la grille est importante. en bas, le fond chauffe plus, en haut, le dessus chauffe plus.
Je vous invite à lire un article que j’ai publié sur le sujet
https://jepensedoncjecuis.com/2019/06/ou-y-t-il-le-plus-de-chaleur-dans-un.html
Et il faut tenir compte de la matière du plat, sachant que le métal transmet plus la chaleur que le verre.
J’espère avoir répondu à votre question. Sinon, n’hésitez pas à revenir vers moi.
Cordialement,
Bonjour,
Je me demande si le poids de l’élément à cuire n’intervient pas quand même un peu dans le temps de cuisson. En effet, quand vous enfournez, vous mettez une masse froide dans le four qui va faire baisser la température; et l’effet est certainement plus significatif pour les temps de cuisson les plus court comme le 1/4 d’heure par livre du boucher ! (que je ne pratique pas). Avec les fours à chaleur ventilée, cet impact doit être limité.
Bonjour,
Merci pour votre question. Pour y répondre, je me suis amusé à faire une petite expérience en préchauffant longtemps mon four à 180°C, et en y mettant à chauffer 500 ml d’eau, puis 2L d’eau dans le même récipient. J’ai contrôlé la température dans le four avec un thermomètre de cuisine.
Résultats : le fait d’ouvrir le four pour y mettre le récipient a fait baisser la température de l’air dans le four, mais elle a mis le même temps pour revenir à 180°C pour les 2 volumes d’eau. Donc la masse d’eau froide n’a pas eu d’effet significatif sur la température dans le four.
Ces résultats sont cohérents avec les informations présentées dans un article sur le fonctionnement des fours (https://jepensedoncjecuis.com/2019/06/ou-y-t-il-le-plus-de-chaleur-dans-un.html) dans lequel j’indique qu’un produit cuit dans un four autant par le rayonnement des parois que par le transfert de chaleur de l’air. D’où l’importance de faire préchauffer longtemps le four, pour avoir un fort rayonnement des parois.
J’espère avoir répondu à votre question. Sinon, n’hésitez pas à revenir vers moi.
Cordialement,
Merci pour la réponse et j’ai lu avec intérêt l’article cité. Très bien et bonne continuation 🙂